WGS84、GCJ02、BD09、CGCS2000、UTM和BJ54地理坐标系详解及免费在线批量转换工具

本文介绍下六种地理坐标系，大地坐标中央经线，以及WGS84、GCJ02、BD09、CGCS2000、UTM五种地理坐标系两两互相转化的Python和Java实现代码，包括十进制和度分秒的互转。并用Next.js开发了一个地图坐标系批量转换免费在线工具，单次最大支持10万条经纬度数据的转化。

一、WGS84

WGS84（World Geodetic System 1984）是全球定位系统（GPS）所使用的地理坐标系统和地球参考框架。它是由美国国防部开发的，广泛应用于导航、制图和地理信息系统（GIS）中。以下是一些关于WGS84坐标系统的重要资料：

1. 基本概念

1. 椭球参数：
   • 长半轴（a）：6378137.0米
   • 扁率倒数（1/f）：298.257223563
   • 短半轴（b）：6356752.3142米
2. 原点：
   • 原点位于地球质心（地球的重心），在赤道和本初子午线的交点处。
3. 坐标系统：
   • 经度（Longitude）：从本初子午线向东或向西测量，范围为-180°到+180°。
   • 纬度（Latitude）：从赤道向北或向南测量，范围为-90°到+90°。
   • 高程（Elevation or Height）：相对于椭球面的高度。

2. 应用领域

1. 导航：用于航空、航海、陆地导航及GPS设备。
2. 制图：地形图、海图、城市地图等都基于WGS84。
3. GIS（地理信息系统）：空间数据分析和管理。
4. 遥感：卫星影像定位和地理数据处理。

3. 转换和比较

WGS84是全球通用的地理坐标系统，但不同的国家和地区可能使用其他的坐标系统，如中国的CGCS2000（中国大地坐标系2000）和日本的JGD2000（日本地理数据2000）。在地理信息处理和应用中，经常需要在不同坐标系统之间进行转换。常见的转换工具包括：

• Proj.4：一个用于转换地理坐标的开源库。
• GDAL（Geospatial Data Abstraction Library）：用于处理和转换地理数据格式的开源库。
• Google Earth：支持多种地理坐标系统的可视化工具。

4. 精度

WGS84不断进行更新以提高其精度。最新的版本是WGS84 (G2139)，其精度在几厘米至几米之间，这取决于具体的应用环境和使用的设备。

5. 参考资料

1. NGA（National Geospatial-Intelligence Agency）发布的WGS84文档。
2. GPS.gov：提供关于GPS及其应用的详细信息。
3. OGC（Open Geospatial Consortium）标准：定义了地理信息系统的数据交换和处理规范。

如果你需要更多关于WGS84的具体技术资料或应用实例，可以访问这些组织的官方网站或相关的技术文档。

二、GCJ02

GCJ-02（火星坐标系）是中国国家测绘局制定的一种地理坐标系统，用于在中国大陆范围内的地理数据。以下是一些关于GCJ-02坐标系统的重要资料和资源链接：

1. 基本概念

1. 椭球参数：
   • GCJ-02的椭球参数与WGS84相同，都是基于地球的椭球模型。
2. 偏移算法：
   • GCJ-02坐标系基于WGS84坐标系进行了一定的加密和偏移处理，以保护国家地理信息安全。
   • 偏移算法是保密的，具体实现未公开，但在开发中有各种实现方法来进行转换。

2. 应用领域

1. 地图服务：高德地图、腾讯地图等中国大陆的地图服务商使用GCJ-02坐标系统。
2. 导航：应用于中国大陆的各种导航设备和服务。
3. 地理信息系统（GIS）：在中国大陆的空间数据处理和管理。

3. 转换工具和库

1. GCoord：一个JavaScript库，用于各种坐标系（包括GCJ-02和WGS84）之间的转换。
   • GCoord GitHub
2. proj4js：一个JavaScript库，用于坐标转换，支持GCJ-02。
   • proj4js GitHub
3. Python Geocoding Libraries：如pyproj库，可用于坐标系转换和地理计算。
   • geopy GitHub

4. 相关标准和规范

1. 国家测绘地理信息局：提供关于GCJ-02的规范和政策。

5. 应用和可视化工具

1. 高德地图：
   • 高德地图官网
2. 腾讯地图：
   • 腾讯地图官网

6. 参考资料

1. GCJ-02和WGS84坐标转换算法：虽然官方算法保密，但网络上有一些第三方提供的转换算法和实现示例。（见文章末尾的示例）

这些链接和资源将提供你关于GCJ-02坐标系统的详细技术资料、使用指南以及相关工具和标准。如果你有特定的需求或应用场景，可以通过这些资源找到更多详细信息和支持。

三、BD09

BD-09（百度坐标系）是百度公司推出的一种地理坐标系统，它基于GCJ-02（火星坐标系）进行进一步的加密和偏移处理。BD-09坐标系广泛应用于百度地图、百度导航等百度提供的地理信息服务中。

1. 基本概念

1. BD-09 坐标系：
   • BD-09 坐标系是在 GCJ-02 坐标系基础上进行进一步偏移处理得到的。
   • 该坐标系通过加密算法对原始坐标进行偏移，以保护地理信息数据的安全。
2. 偏移算法：
   • BD-09 的具体加密算法未公开，但有公开的第三方实现和逆向工程结果。

2. 应用领域

1. 地图服务：百度地图等基于百度坐标系进行展示和导航。
2. 导航服务：百度导航在中国大陆范围内使用 BD-09 坐标系进行定位和导航。
3. 地理信息系统（GIS）：百度提供的地理数据和服务采用 BD-09 坐标系。

3. 转换工具和库

1. Python 坐标转换库：如pyproj库，可用于坐标系转换和地理计算。
   • pyproj Documentation
2. 坐标转换算法示例：提供 WGS84、GCJ-02 和 BD-09 坐标系之间的转换算法。（见文章尾部示例）
3. GCoord：一个 JavaScript 库，用于各种坐标系（包括 BD-09、GCJ-02 和 WGS84）之间的转换。
   • GCoord GitHub

4. 相关标准和规范

1. 国家测绘地理信息局：提供关于地理坐标系的规范和政策。

5. 应用和可视化工具

1. 百度地图：
   • 百度地图官网
2. 百度开发者平台：提供百度地图相关的开发文档和 API。
   • 百度开发者平台

6. 参考资料

1. 百度地图 API 文档：提供关于 BD-09 坐标系使用和转换的详细说明。
   • 百度地图 API 文档
2. GCJ-02 和 BD-09 坐标转换算法：虽然官方算法保密，但网络上有一些第三方提供的转换算法和实现示例。（见文章末尾的示例）

这些链接和资源将提供你关于 BD-09 坐标系统的详细技术资料、使用指南以及相关工具和标准。如果你有特定的需求或应用场景，可以通过这些资源找到更多详细信息和支持。

四、CGCS2000

CGCS2000（China Geodetic Coordinate System 2000）是中国大地坐标系2000，是中国国家测绘地理信息局（NGCC）建立的地理坐标系，广泛应用于国家测绘、地理信息系统（GIS）和导航等领域。

1. 基本概念

1. 参考椭球参数：
   • 长半轴（a）：6378137.0米
   • 扁率倒数（1/f）：298.257222101
   • 地心引力常数　GM＝3.986004418×1014m3s-2
   • 自转角速度　ω＝7.292l15×10-5rad s-1
2. 原点：
   • 原点位于地球质心，参照国际大地参考框架（ITRF）。
3. 坐标系统：
   • 经度（Longitude）：从本初子午线向东或向西测量，范围为-180°到+180°。
   • 纬度（Latitude）：从赤道向北或向南测量，范围为-90°到+90°。
   • 高程（Elevation or Height）：相对于椭球面的高度。

2. 应用领域

1. 测绘：国家大地测量、工程测量和基础地理信息数据采集。
2. 导航：北斗导航系统和其他导航设备。
3. GIS：空间数据分析、城市规划和资源管理等。

3. 转换工具和库

1. Proj.4：一个用于坐标转换的开源库，支持CGCS2000和其他常见坐标系。
   • Proj.4 Documentation
2. GDAL（Geospatial Data Abstraction Library）：用于处理和转换地理数据格式的开源库。
   • GDAL Documentation
3. 中国国家测绘地理信息局：提供CGCS2000的标准和技术规范。
   • 中国国家测绘地理信息局

4. 相关标准和规范

1. CGCS2000 坐标系技术规定：详细定义了CGCS2000的技术细节和应用规范。
2. ITRF（International Terrestrial Reference Frame）：CGCS2000是基于ITRF的坐标系。

5. 应用和可视化工具

1. ArcGIS：支持CGCS2000坐标系的GIS软件。
2. QGIS：开源GIS软件，支持CGCS2000坐标系。

6. 参考资料

1. CGCS2000 介绍：详细介绍CGCS2000坐标系的文章和文档。
2. 测绘科学研究院：提供关于CGCS2000的研究和应用信息。

这些链接和资源将提供你关于CGCS2000坐标系统的详细技术资料、使用指南以及相关工具和标准。如果你有特定的需求或应用场景，可以通过这些资源找到更多详细信息和支持。

五、UTM

1. 什么是UTM坐标系？

UTM（Universal Transverse Mercator）坐标系是基于横轴墨卡托投影的一种地理坐标系，将地球表面划分为多个投影带，每个投影带覆盖6度经度范围。UTM坐标系以米为单位，用来表示地理位置。

2. UTM坐标系的特点

1. 分区：
   • 地球表面被划分为60个纵向带区，每个带区宽6度经度。
   • 带区编号从西经180度开始，从1到60。
   • 每个带区又进一步划分为北半球和南半球。
2. 坐标表示：
   • 东向偏移（Easting）：从带区中央经线开始，向东以米为单位计量。中央经线的东向偏移通常设为500,000米，以避免负值。
   • 北向偏移（Northing）：从赤道开始，向北以米为单位计量。在北半球从赤道开始计量；在南半球，赤道的北向偏移设为10,000,000米，以避免负值。

3. UTM坐标格式

一个典型的UTM坐标由以下部分组成：

• 东向偏移（Easting）：以米为单位，从带区中央经线开始。
• 北向偏移（Northing）：以米为单位，从赤道开始。
• 带区编号（Zone Number）：表示经度范围，从1到60。
• 带区字母（Zone Letter）：表示纬度范围，从C到X（不包括I和O），每个字母带区的纬度范围为8度。

4. 示例：

例如，以下是一个UTM坐标的示例：

• 东向偏移：500,000米
• 北向偏移：4,649,776米
• 带区编号：33
• 带区字母：T

5. UTM和WGS84格式之间的转换

常规处理默认是使用6度分带，在某些情况下，为了提高精度，可以使用3度分带的UTM坐标系，即每个带区宽3度经度，而不是通常的6度。这种情况下，带区编号的范围会变成1到120。

六、BJ54

BJ54（北京1954坐标系）是中国在1954年建立的大地坐标系统，它基于克拉索夫斯基椭球（Krasovsky ellipsoid）并广泛应用于中国的测绘和地理信息系统中，特别是在CGCS2000（中国大地坐标系2000）建立之前。以下是有关BJ54坐标系的详细信息及相关链接资源。

基本概念

1. 椭球参数：
   • 长半轴（a）：6378245.0米
   • 扁率倒数（1/f）：298.3
2. 投影方式：
   • BJ54常使用高斯-克吕格（Gauss-Krüger）投影，将地理坐标转换为平面坐标。
   • 在高斯-克吕格投影中，中国通常使用6度分带。
3. 参考大地原点：
   • 原点设在北京观象台（北纬39°54′40.90″，东经116°27′43.95″）。

应用领域

1. 测绘：20世纪中期至21世纪初，中国的大部分测绘工作都是基于BJ54坐标系进行的。
2. 工程测量：在CGCS2000坐标系普及之前，BJ54坐标系被广泛用于工程测量和国土资源管理。
3. 地理信息系统（GIS）：早期的GIS数据通常使用BJ54坐标系存储和分析。

转换工具和库

1. Proj.4：一个用于坐标转换的开源库，支持BJ54坐标系与其他坐标系的转换。
   • Proj.4 Documentation
2. GDAL（Geospatial Data Abstraction Library）：支持多种坐标系转换，包括BJ54。
   • GDAL Documentation
3. 中国国家测绘地理信息局：提供中国坐标系的标准和技术规范。
   • 中国国家测绘地理信息局

相关标准和规范

1. 国家标准：关于BJ54坐标系的使用和技术规范。
   • 中国国家测绘地理信息局的标准
2. 地理坐标系转换标准：描述了BJ54和其他坐标系之间的转换方法和公式。
   • 测绘科学研究院

应用和可视化工具

1. ArcGIS：支持BJ54坐标系的GIS软件。
   • ArcGIS
2. QGIS：开源GIS软件，支持BJ54坐标系。
   • QGIS

参考资料

1. 中国测绘科学研究院：提供关于BJ54的研究和应用信息。
   • 中国测绘科学研究院

这些链接和资源将提供你关于BJ54坐标系统的详细技术资料、使用指南以及相关工具和标准。如果你有特定的需求或应用场景，可以通过这些资源找到更多详细信息和支持。

七、大地坐标中央经线

在大地坐标转换中，6度分带和3度分带的参数主要用于高斯-克吕格（Gauss-Krüger）投影和UTM（Universal Transverse Mercator）投影。这些投影方法将球面坐标转换为平面坐标，适用于大比例尺地图制图和精确的地理信息系统（GIS）分析。在WGS84、GCJ-02、BD-09和CGCS2000坐标系之间的转换中，6度分带和3度分带的参数并不直接使用，因为这些转换主要是地理坐标系之间的转换，而不是投影坐标系之间的转换。

1. 中央经线参考表信息

中央经线参考表在高斯-克吕格投影和UTM投影中起关键作用。这些参考表提供了不同分带系统下各带的中央经线值：

• 6度分带：
  • 每个带宽6度，中央经线从3度起始，以6度递增。
  • 例如，第一个带的中央经线是3度，第二个带是9度，依此类推。
• 3度分带：
  • 每个带宽3度，中央经线从1.5度起始，以3度递增。
  • 例如，第一个带的中央经线是1.5度，第二个带是4.5度，依此类推。

2. 在坐标系转换中的使用

在直接进行WGS84、GCJ-02、BD-09和CGCS2000地理坐标系之间的转换时，不涉及平面坐标系（如高斯-克吕格或UTM）的转换，因此不需要使用6度分带和3度分带的参数。这些转换主要涉及椭球参数和偏移算法。

然而，如果你需要将地理坐标转换为平面坐标，或者将平面坐标转换为地理坐标，则需要使用6度分带和3度分带的参数。常规的处理默认使用标准的6度分带，如果需要使用3度分带，需要自定义转换逻辑，例如：

1. 从地理坐标（WGS84）到UTM坐标：
   • 需要确定地理坐标所在的UTM带，并使用该带的中央经线进行投影转换。
2. 从UTM坐标到地理坐标（WGS84）：
   • 需要使用相应的中央经线和带宽参数将平面坐标转换回地理坐标。

3. 举例说明

例如，在使用高斯-克吕格投影时，转换步骤可能包括：

1. 地理坐标到高斯-克吕格平面坐标：
   • 确定分带（6度或3度），找到对应的中央经线。
   • 使用高斯-克吕格投影公式将地理坐标转换为平面坐标。
2. 高斯-克吕格平面坐标到地理坐标：
   • 使用相应的中央经线和分带信息，应用逆高斯-克吕格公式将平面坐标转换回地理坐标。

总之，6度分带和3度分带的参数在高斯-克吕格和UTM投影中至关重要，但在纯地理坐标系（如WGS84、GCJ-02、BD-09、CGCS2000）之间的转换中不需要使用这些参数。如果你的应用涉及到从地理坐标到投影坐标的转换（或反之），则需要考虑这些分带参数。

4. 6度分带

带号	经度范围	中央经线
1	-180° to -174°	-177
2	-174° to -168°	-171
3	-168° to -162°	-165
4	-162° to -156°	-159
5	-156° to -150°	-153
6	-150° to -144°	-147
7	-144° to -138°	-141
8	-138° to -132°	-135
9	-132° to -126°	-129
10	-126° to -120°	-123
11	-120° to -114°	-117
12	-114° to -108°	-111
13	-108° to -102°	-105
14	-102° to -96°	-99
15	-96° to -90°	-93
16	-90° to -84°	-87
17	-84° to -78°	-81
18	-78° to -72°	-75
19	-72° to -66°	-69
20	-66° to -60°	-63
21	-60° to -54°	-57
22	-54° to -48°	-51
23	-48° to -42°	-45
24	-42° to -36°	-39
25	-36° to -30°	-33
26	-30° to -24°	-27
27	-24° to -18°	-21
28	-18° to -12°	-15
29	-12° to -6°	-9
30	-6° to 0°	-3
31	0° to 6°	3
32	6° to 12°	9
33	12° to 18°	15
34	18° to 24°	21
35	24° to 30°	27
36	30° to 36°	33
37	36° to 42°	39
38	42° to 48°	45
39	48° to 54°	51
40	54° to 60°	57
41	60° to 66°	63
42	66° to 72°	69
43	72° to 78°	75
44	78° to 84°	81
45	84° to 90°	87
46	90° to 96°	93
47	96° to 102°	99
48	102° to 108°	105
49	108° to 114°	111
50	114° to 120°	117
51	120° to 126°	123
52	126° to 132°	129
53	132° to 138°	135
54	138° to 144°	141
55	144° to 150°	147
56	150° to 156°	153
57	156° to 162°	159
58	162° to 168°	165
59	168° to 174°	171
60	174° to 180°	177

5. 3度分带

带号 (Zone Number)	经度范围 (Longitude Range)	中央经线 (Central Meridian)
1	-1.5°E ~ 1.5°E	0°E
2	1.5°E ~ 4.5°E	3°E
3	4.5°E ~ 7.5°E	6°E
4	7.5°E ~ 10.5°E	9°E
5	10.5°E ~ 13.5°E	12°E
6	13.5°E ~ 16.5°E	15°E
7	16.5°E ~ 19.5°E	18°E
8	19.5°E ~ 22.5°E	21°E
9	22.5°E ~ 25.5°E	24°E
10	25.5°E ~ 28.5°E	27°E
11	28.5°E ~ 31.5°E	30°E
12	31.5°E ~ 34.5°E	33°E
13	34.5°E ~ 37.5°E	36°E
14	37.5°E ~ 40.5°E	39°E
15	40.5°E ~ 43.5°E	42°E
16	43.5°E ~ 46.5°E	45°E
17	46.5°E ~ 49.5°E	48°E
18	49.5°E ~ 52.5°E	51°E
19	52.5°E ~ 55.5°E	54°E
20	55.5°E ~ 58.5°E	57°E
21	58.5°E ~ 61.5°E	60°E
22	61.5°E ~ 64.5°E	63°E
23	64.5°E ~ 67.5°E	66°E
24	67.5°E ~ 70.5°E	69°E
25	70.5°E ~ 73.5°E	72°E
26	73.5°E ~ 76.5°E	75°E
27	76.5°E ~ 79.5°E	78°E
28	79.5°E ~ 82.5°E	81°E
29	82.5°E ~ 85.5°E	84°E
30	85.5°E ~ 88.5°E	87°E
31	88.5°E ~ 91.5°E	90°E
32	91.5°E ~ 94.5°E	93°E
33	94.5°E ~ 97.5°E	96°E
34	97.5°E ~ 100.5°E	99°E
35	100.5°E ~ 103.5°E	102°E
36	103.5°E ~ 106.5°E	105°E
37	106.5°E ~ 109.5°E	108°E
38	109.5°E ~ 112.5°E	111°E
39	112.5°E ~ 115.5°E	114°E
40	115.5°E ~ 118.5°E	117°E
41	118.5°E ~ 121.5°E	120°E
42	121.5°E ~ 124.5°E	123°E
43	124.5°E ~ 127.5°E	126°E
44	127.5°E ~ 130.5°E	129°E
45	130.5°E ~ 133.5°E	132°E
46	133.5°E ~ 136.5°E	135°E
47	136.5°E ~ 139.5°E	138°E
48	139.5°E ~ 142.5°E	141°E
49	142.5°E ~ 145.5°E	144°E
50	145.5°E ~ 148.5°E	147°E
51	148.5°E ~ 151.5°E	150°E
52	151.5°E ~ 154.5°E	153°E
53	154.5°E ~ 157.5°E	156°E
54	157.5°E ~ 160.5°E	159°E
55	160.5°E ~ 163.5°E	162°E
56	163.5°E ~ 166.5°E	165°E
57	166.5°E ~ 169.5°E	168°E
58	169.5°E ~ 172.5°E	171°E
59	172.5°E ~ 175.5°E	174°E
60	175.5°E ~ 178.5°E	177°E
61	178.5°E ~ 181.5°E	180°E
62	181.5°E ~ 184.5°E	183°E
63	184.5°E ~ 187.5°E	186°E
64	187.5°E ~ 190.5°E	189°E
65	190.5°E ~ 193.5°E	192°E
66	193.5°E ~ 196.5°E	195°E
67	196.5°E ~ 199.5°E	198°E
68	199.5°E ~ 202.5°E	201°E
69	202.5°E ~ 205.5°E	204°E
70	205.5°E ~ 208.5°E	207°E
71	208.5°E ~ 211.5°E	210°E
72	211.5°E ~ 214.5°E	213°E
73	214.5°E ~ 217.5°E	216°E
74	217.5°E ~ 220.5°E	219°E
75	220.5°E ~ 223.5°E	222°E
76	223.5°E ~ 226.5°E	225°E
77	226.5°E ~ 229.5°E	228°E
78	229.5°E ~ 232.5°E	231°E
79	232.5°E ~ 235.5°E	234°E
80	235.5°E ~ 238.5°E	237°E
81	238.5°E ~ 241.5°E	240°E
82	241.5°E ~ 244.5°E	243°E
83	244.5°E ~ 247.5°E	246°E
84	247.5°E ~ 250.5°E	249°E
85	250.5°E ~ 253.5°E	252°E
86	253.5°E ~ 256.5°E	255°E
87	256.5°E ~ 259.5°E	258°E
88	259.5°E ~ 262.5°E	261°E
89	262.5°E ~ 265.5°E	264°E
90	265.5°E ~ 268.5°E	267°E
91	268.5°E ~ 271.5°E	270°E
92	271.5°E ~ 274.5°E	273°E
93	274.5°E ~ 277.5°E	276°E
94	277.5°E ~ 280.5°E	279°E
95	280.5°E ~ 283.5°E	282°E
96	283.5°E ~ 286.5°E	285°E
97	286.5°E ~ 289.5°E	288°E
98	289.5°E ~ 292.5°E	291°E
99	292.5°E ~ 295.5°E	294°E
100	295.5°E ~ 298.5°E	297°E
101	298.5°E ~ 301.5°E	300°E
102	301.5°E ~ 304.5°E	303°E
103	304.5°E ~ 307.5°E	306°E
104	307.5°E ~ 310.5°E	309°E
105	310.5°E ~ 313.5°E	312°E
106	313.5°E ~ 316.5°E	315°E
107	316.5°E ~ 319.5°E	318°E
108	319.5°E ~ 322.5°E	321°E
109	322.5°E ~ 325.5°E	324°E
110	325.5°E ~ 328.5°E	327°E
111	328.5°E ~ 331.5°E	330°E
112	331.5°E ~ 334.5°E	333°E
113	334.5°E ~ 337.5°E	336°E
114	337.5°E ~ 340.5°E	339°E
115	340.5°E ~ 343.5°E	342°E
116	343.5°E ~ 346.5°E	345°E
117	346.5°E ~ 349.5°E	348°E
118	349.5°E ~ 352.5°E	351°E
119	352.5°E ~ 355.5°E	354°E
120	355.5°E ~ 358.5°E	357°E

八、坐标系转化示例代码

以下是WGS84、GCJ-02、BD-09、CGCS2000、UTM、DMS(度分秒)和Decimal(十进制)坐标系之间互相转换的示例代码实现，分别用Java和Python实现。

1. Java 实现

import org.geotools.referencing.CRS;
import org.geotools.referencing.crs.DefaultGeographicCRS;
import org.geotools.referencing.operation.MathTransform;
import org.opengis.referencing.FactoryException;
import org.opengis.referencing.NoSuchAuthorityCodeException;
import org.opengis.referencing.operation.TransformException;

public class CoordinateTransform {

    private static final double PI = 3.1415926535897932384626;
    private static final double X_PI = PI * 3000.0 / 180.0;
    private static final double A = 6378245.0;
    private static final double EE = 0.00669342162296594323;

    // WGS84 to GCJ-02
    public static double[] wgs84ToGcj02(double lat, double lon) {
        if (outOfChina(lat, lon)) {
            return new double[]{lat, lon};
        }
        double dLat = transformLat(lon - 105.0, lat - 35.0);
        double dLon = transformLon(lon - 105.0, lat - 35.0);
        double radLat = lat / 180.0 * PI;
        double magic = Math.sin(radLat);
        magic = 1 - EE * magic * magic;
        double sqrtMagic = Math.sqrt(magic);
        dLat = (dLat * 180.0) / ((A * (1 - EE)) / (magic * sqrtMagic) * PI);
        dLon = (dLon * 180.0) / (A / sqrtMagic * Math.cos(radLat) * PI);
        double mgLat = lat + dLat;
        double mgLon = lon + dLon;
        return new double[]{mgLat, mgLon};
    }

    // GCJ-02 to WGS84
    public static double[] gcj02ToWgs84(double lat, double lon) {
        double[] gcj02 = wgs84ToGcj02(lat, lon);
        double dLat = gcj02[0] - lat;
        double dLon = gcj02[1] - lon;
        return new double[]{lat - dLat, lon - dLon};
    }

    // GCJ-02 to BD-09
    public static double[] gcj02ToBd09(double lat, double lon) {
        double z = Math.sqrt(lon * lon + lat * lat) + 0.00002 * Math.sin(lat * X_PI);
        double theta = Math.atan2(lat, lon) + 0.000003 * Math.cos(lon * X_PI);
        double bdLon = z * Math.cos(theta) + 0.0065;
        double bdLat = z * Math.sin(theta) + 0.006;
        return new double[]{bdLat, bdLon};
    }

    // BD-09 to GCJ-02
    public static double[] bd09ToGcj02(double lat, double lon) {
        double x = lon - 0.0065;
        double y = lat - 0.006;
        double z = Math.sqrt(x * x + y * y) - 0.00002 * Math.sin(y * X_PI);
        double theta = Math.atan2(y, x) - 0.000003 * Math.cos(x * X_PI);
        double gcjLon = z * Math.cos(theta);
        double gcjLat = z * Math.sin(theta);
        return new double[]{gcjLat, gcjLon};
    }

    // WGS84 to BD-09
    public static double[] wgs84ToBd09(double lat, double lon) {
        double[] gcj02 = wgs84ToGcj02(lat, lon);
        return gcj02ToBd09(gcj02[0], gcj02[1]);
    }

    // BD-09 to WGS84
    public static double[] bd09ToWgs84(double lat, double lon) {
        double[] gcj02 = bd09ToGcj02(lat, lon);
        return gcj02ToWgs84(gcj02[0], gcj02[1]);
    }

    // CGCS2000 to WGS84
    public static double[] cgcs2000ToWgs84(double lat, double lon) {
        return new double[]{lat, lon}; // Assume CGCS2000 is equivalent to WGS84 for simplicity
    }

    // WGS84 to CGCS2000
    public static double[] wgs84ToCgcs2000(double lat, double lon) {
        return new double[]{lat, lon}; // Assume CGCS2000 is equivalent to WGS84 for simplicity
    }

    // GCJ-02 to CGCS2000
    public static double[] gcj02ToCgcs2000(double lat, double lon) {
        double[] wgs84 = gcj02ToWgs84(lat, lon);
        return wgs84ToCgcs2000(wgs84[0], wgs84[1]);
    }

    // CGCS2000 to GCJ-02
    public static double[] cgcs2000ToGcj02(double lat, double lon) {
        double[] wgs84 = cgcs2000ToWgs84(lat, lon);
        return wgs84ToGcj02(wgs84[0], wgs84[1]);
    }

    // WGS84 to UTM
    public static UTMResult WGS84ToUTM(double latitude, double longitude) throws NoSuchAuthorityCodeException, FactoryException, TransformException {
        int zoneNumber = (int) Math.floor((longitude + 180) / 6) + 1;
        boolean isNorthernHemisphere = latitude >= 0;
        String utmCRS = "EPSG:" + (isNorthernHemisphere ? "326" : "327") + zoneNumber;

        MathTransform transform = CRS.findMathTransform(DefaultGeographicCRS.WGS84, CRS.decode(utmCRS));
        double[] src = new double[]{longitude, latitude};
        double[] dest = new double[2];
        transform.transform(src, 0, dest, 0, 1);

        char zoneLetter = getUTMLetterDesignator(latitude);
        return new UTMResult(dest[0], dest[1], zoneNumber, zoneLetter);
    }

    // UTM to WGS84
    public static double[] UTMToWGS84(double easting, double northing, int zoneNumber, char zoneLetter) throws NoSuchAuthorityCodeException, FactoryException, TransformException {
        boolean isNorthernHemisphere = (zoneLetter >= 'N');
        String utmCRS = "EPSG:" + (isNorthernHemisphere ? "326" : "327") + zoneNumber;

        MathTransform transform = CRS.findMathTransform(CRS.decode(utmCRS), DefaultGeographicCRS.WGS84);
        double[] src = new double[]{easting, northing};
        double[] dest = new double[2];
        transform.transform(src, 0, dest, 0, 1);

        return dest;
    }

    private static char getUTMLetterDesignator(double latitude) {
        if ((84 >= latitude) && (latitude >= 72)) return 'X';
        else if ((72 > latitude) && (latitude >= 64)) return 'W';
        else if ((64 > latitude) && (latitude >= 56)) return 'V';
        else if ((56 > latitude) && (latitude >= 48)) return 'U';
        else if ((48 > latitude) && (latitude >= 40)) return 'T';
        else if ((40 > latitude) && (latitude >= 32)) return 'S';
        else if ((32 > latitude) && (latitude >= 24)) return 'R';
        else if ((24 > latitude) && (latitude >= 16)) return 'Q';
        else if ((16 > latitude) && (latitude >= 8)) return 'P';
        else if ((8 > latitude) && (latitude >= 0)) return 'N';
        else if ((0 > latitude) && (latitude >= -8)) return 'M';
        else if ((-8 > latitude) && (latitude >= -16)) return 'L';
        else if ((-16 > latitude) && (latitude >= -24)) return 'K';
        else if ((-24 > latitude) && (latitude >= -32)) return 'J';
        else if ((-32 > latitude) && (latitude >= -40)) return 'H';
        else if ((-40 > latitude) && (latitude >= -48)) return 'G';
        else if ((-48 > latitude) && (latitude >= -56)) return 'F';
        else if ((-56 > latitude) && (latitude >= -64)) return 'E';
        else if ((-64 > latitude) && (latitude >= -72)) return 'D';
        else if ((-72 > latitude) && (latitude >= -80)) return 'C';
        else return 'Z'; // Latitude is outside the UTM limits
    }

    static class UTMResult {
        double easting;
        double northing;
        int zoneNumber;
        char zoneLetter;

        public UTMResult(double easting, double northing, int zoneNumber, char zoneLetter) {
            this.easting = easting;
            this.northing = northing;
            this.zoneNumber = zoneNumber;
            this.zoneLetter = zoneLetter;
        }
    }

    // DMS to Decimal
    public static double[] dmsToDecimal(String dmsLat, String dmsLon) {
        double lat = convertDMSToDecimal(dmsLat);
        double lon = convertDMSToDecimal(dmsLon);
        return new double[]{lat, lon};
    }

    private static double convertDMSToDecimal(String dms) {
        String[] dmsParts = dms.split("[°'\"]");
        double degrees = Double.parseDouble(dmsParts[0]);
        double minutes = Double.parseDouble(dmsParts[1]);
        double seconds = Double.parseDouble(dmsParts[2]);
        String direction = dmsParts[3];

        double decimal = degrees + (minutes / 60) + (seconds / 3600);
        if (direction.equals("S") || direction.equals("W")) {
            decimal *= -1;
        }
        return decimal;
    }
    
    // Decimal to DMS 
    public static String[] decimalToDMS(double decimalLat, double decimalLon) {
        String latDMS = convertDecimalToDMS(decimalLat, true);
        String lonDMS = convertDecimalToDMS(decimalLon, false);
        return new String[]{latDMS, lonDMS};
    }

    private static String convertDecimalToDMS(double decimal, boolean isLatitude) {
        String direction;
        if (isLatitude) {
            direction = decimal >= 0 ? "N" : "S";
        } else {
            direction = decimal >= 0 ? "E" : "W";
        }
        decimal = Math.abs(decimal);
        int degrees = (int) decimal;
        double minutesNotTruncated = (decimal - degrees) * 60;
        int minutes = (int) minutesNotTruncated;
        double seconds = (minutesNotTruncated - minutes) * 60;
        return degrees + "°" + minutes + "'" + String.format("%.2f", seconds) + "\"" + direction;
    }

    private static boolean outOfChina(double lat, double lon) {
        return (lon < 72.004 || lon > 137.8347) || (lat < 0.8293 || lat > 55.8271);
    }

    private static double transformLat(double x, double y) {
        double ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y + 0.2 * Math.sqrt(Math.abs(x));
        ret += (20.0 * Math.sin(6.0 * x * PI) + 20.0 * Math.sin(2.0 * x * PI)) * 2.0 / 3.0;
        ret += (20.0 * Math.sin(y * PI) + 40.0 * Math.sin(y / 3.0 * PI)) * 2.0 / 3.0;
        ret += (160.0 * Math.sin(y / 12.0 * PI) + 320.0 * Math.sin(y * PI / 30.0)) * 2.0 / 3.0;
        return ret;
    }

    private static double transformLon(double x, double y) {
        double ret = 300.0 + x + 2.0 * y + 0.1 * x * x + 0.1 * x * y + 0.1 * Math.sqrt(Math.abs(x));
        ret += (20.0 * Math.sin(6.0 * x * PI) + 20.0 * Math.sin(2.0 * x * PI)) * 2.0 / 3.0;
        ret += (20.0 * Math.sin(x * PI) + 40.0 * Math.sin(x / 3.0 * PI)) * 2.0 / 3.0;
        ret += (150.0 * Math.sin(x / 12.0 * PI) + 300.0 * Math.sin(x / 30.0 * PI)) * 2.0 / 3.0;
        return ret;
    }

    public static void main(String[] args) {
        double lat = 39.90960456049752;
        double lon = 116.3972282409668;

        // WGS84 to GCJ-02
        double[] gcj02 = wgs84ToGcj02(lat, lon);
        System.out.println("WGS84 to GCJ-02: " + gcj02[0] + ", " + gcj02[1]);

        // GCJ-02 to BD-09
        double[] bd09 = gcj02ToBd09(gcj02[0], gcj02[1]);
        System.out.println("GCJ-02 to BD-09: " + bd09[0] + ", " + bd09[1]);

        // BD-09 to GCJ-02
        double[] gcj02FromBd09 = bd09ToGcj02(bd09[0], bd09[1]);
        System.out.println("BD-09 to GCJ-02: " + gcj02FromBd09[0] + ", " + gcj02FromBd09[1]);

        // GCJ-02 to WGS84
        double[] wgs84FromGcj02 = gcj02ToWgs84(gcj02FromBd09[0], gcj02FromBd09[1]);
        System.out.println("GCJ-02 to WGS84: " + wgs84FromGcj02[0] + ", " + wgs84FromGcj02[1]);

        // WGS84 to BD-09
        double[] bd09FromWgs84 = wgs84ToBd09(lat, lon);
        System.out.println("WGS84 to BD-09: " + bd09FromWgs84[0] + ", " + bd09FromWgs84[1]);

        // BD-09 to WGS84
        double[] wgs84FromBd09 = bd09ToWgs84(bd09FromWgs84[0], bd09FromWgs84[1]);
        System.out.println("BD-09 to WGS84: " + wgs84FromBd09[0] + ", " + wgs84FromBd09[1]);

        // CGCS2000 to WGS84
        double[] wgs84FromCgcs2000 = cgcs2000ToWgs84(lat, lon);
        System.out.println("CGCS2000 to WGS84: " + wgs84FromCgcs2000[0] + ", " + wgs84FromCgcs2000[1]);

        // WGS84 to CGCS2000
        double[] cgcs2000FromWgs84 = wgs84ToCgcs2000(lat, lon);
        System.out.println("WGS84 to CGCS2000: " + cgcs2000FromWgs84[0] + ", " + cgcs2000FromWgs84[1]);

        // GCJ-02 to CGCS2000
        double[] cgcs2000FromGcj02 = gcj02ToCgcs2000(gcj02[0], gcj02[1]);
        System.out.println("GCJ-02 to CGCS2000: " + cgcs2000FromGcj02[0] + ", " + cgcs2000FromGcj02[1]);

        // CGCS2000 to GCJ-02
        double[] gcj02FromCgcs2000 = cgcs2000ToGcj02(lat, lon);
        System.out.println("CGCS2000 to GCJ-02: " + gcj02FromCgcs2000[0] + ", " + gcj02FromCgcs2000[1]);

        // WGS84 to UTM
        UTMResult utm = WGS84ToUTM(lat, lon);
        System.out.println("UTM: Easting: " + utm.easting + ", Northing: " + utm.northing + ", Zone Number: " + utm.zoneNumber + ", Zone Letter: " + utm.zoneLetter);

        // UTM to WGS84
        double[] wgs84 = UTMToWGS84(utm.easting, utm.northing, utm.zoneNumber, utm.zoneLetter);
        System.out.println("WGS84: Latitude: " + wgs84[0] + ", Longitude: " + wgs84[1]);

        // DMS to Decimal
        String dmsLat = "23°3'3.78\"N";
        String dmsLon = "113°22'17.36\"E";
        double[] decimalCoords = dmsToDecimal(dmsLat, dmsLon);
        System.out.println("Decimal: Latitude: " + decimalCoords[0] + ", Longitude: " + decimalCoords[1]);
        
        // Decimal to DMS
        String[] dmsCoords = decimalToDMS(lat, lon);
        System.out.println("DMS: Latitude: " + dmsCoords[0] + ", Longitude: " + dmsCoords[1]);
    }
}

2. Python实现

import math
import utm

X_PI = 3.14159265358979324 * 3000.0 / 180.0
PI = 3.1415926535897932384626
A = 6378245.0
EE = 0.00669342162296594323

def transformLat(x, y):
    ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y + 0.2 * math.sqrt(abs(x))
    ret += (20.0 * math.sin(6.0 * x * PI) + 20.0 * math.sin(2.0 * x * PI)) * 2.0 / 3.0
    ret += (20.0 * math.sin(y * PI) + 40.0 * math.sin(y / 3.0 * PI)) * 2.0 / 3.0
    ret += (160.0 * math.sin(y / 12.0 * PI) + 320.0 * math.sin(y * PI / 30.0)) * 2.0 / 3.0
    return ret

def transformLon(x, y):
    ret = 300.0 + x + 2.0 * y + 0.1 * x * x + 0.1 * x * y + 0.1 * math.sqrt(abs(x))
    ret += (20.0 * math.sin(6.0 * x * PI) + 20.0 * math.sin(2.0 * x * PI)) * 2.0 / 3.0
    ret += (20.0 * math.sin(x * PI) + 40.0 * math.sin(x / 3.0 * PI)) * 2.0 / 3.0
    ret += (150.0 * math.sin(x / 12.0 * PI) + 300.0 * math.sin(x / 30.0 * PI)) * 2.0 / 3.0
    return ret

def wgs84_to_gcj02(lat, lon):
    if out_of_china(lat, lon):
        return lat, lon
    dLat = transformLat(lon - 105.0, lat - 35.0)
    dLon = transformLon(lon - 105.0, lat - 35.0)
    radLat = lat / 180.0 * PI
    magic = math.sin(radLat)
    magic = 1 - EE * magic * magic
    sqrtMagic = math.sqrt(magic)
    dLat = (dLat * 180.0) / ((A * (1 - EE)) / (magic * sqrtMagic) * PI)
    dLon = (dLon * 180.0) / (A / sqrtMagic * math.cos(radLat) * PI)
    mgLat = lat + dLat
    mgLon = lon + dLon
    return mgLat, mgLon

def gcj02_to_wgs84(lat, lon):
    gcj02 = wgs84_to_gcj02(lat, lon)
    dLat = gcj02[0] - lat
    dLon = gcj02[1] - lon
    return lat - dLat, lon - dLon

def gcj02_to_bd09(lat, lon):
    z = math.sqrt(lon * lon + lat * lat) + 0.00002 * math.sin(lat * X_PI)
    theta = math.atan2(lat, lon) + 0.000003 * math.cos(lon * X_PI)
    bd_lon = z * math.cos(theta) + 0.0065
    bd_lat = z * math.sin(theta) + 0.006
    return bd_lat, bd_lon

def bd09_to_gcj02(lat, lon):
    x = lon - 0.0065
    y = lat - 0.006
    z = math.sqrt(x * x + y * y) - 0.00002 * math.sin(y * X_PI)
    theta = math.atan2(y, x) - 0.000003 * math.cos(x * X_PI)
    gcj_lon = z * math.cos(theta)
    gcj_lat = z * math.sin(theta)
    return gcj_lat, gcj_lon

def wgs84_to_bd09(lat, lon):
    gcj02 = wgs84_to_gcj02(lat, lon)
    return gcj02_to_bd09(gcj02[0], gcj02[1])

def bd09_to_wgs84(lat, lon):
    gcj02 = bd09_to_gcj02(lat, lon)
    return gcj02_to_wgs84(gcj02[0], gcj02[1])

def cgcs2000_to_wgs84(lat, lon):
    return lat, lon  # Assume CGCS2000 is equivalent to WGS84 for simplicity

def wgs84_to_cgcs2000(lat, lon):
    return lat, lon  # Assume CGCS2000 is equivalent to WGS84 for simplicity

def gcj02_to_cgcs2000(lat, lon):
    wgs84 = gcj02_to_wgs84(lat, lon)
    return wgs84_to_cgcs2000(wgs84[0], wgs84[1])

def cgcs2000_to_gcj02(lat, lon):
    wgs84 = cgcs2000_to_wgs84(lat, lon)
    return wgs84_to_gcj02(wgs84[0], wgs84[1])

# WGS84 to UTM
def WGS84ToUTM(latitude, longitude):
    u = utm.from_latlon(latitude, longitude)
    return u

# UTM to WGS84
def UTMToWGS84(easting, northing, zone_number, zone_letter):
    latlon = utm.to_latlon(easting, northing, zone_number, zone_letter)
    return latlon

def dms_to_decimal(dms_lat, dms_lon):
    lat = convert_dms_to_decimal(dms_lat)
    lon = convert_dms_to_decimal(dms_lon)
    return lat, lon

def convert_dms_to_decimal(dms):
    degrees, minutes, seconds, direction = re.split('[°\'"]', dms)
    decimal = float(degrees) + float(minutes) / 60 + float(seconds) / 3600
    if direction in ['S', 'W']:
        decimal *= -1
    return decimal

def decimal_to_dms(decimal_lat, decimal_lon):
    lat_dms = convert_decimal_to_dms(decimal_lat, True)
    lon_dms = convert_decimal_to_dms(decimal_lon, False)
    return lat_dms, lon_dms

def convert_decimal_to_dms(decimal, is_latitude):
    direction = 'N' if is_latitude else 'E'
    if decimal < 0:
        direction = 'S' if is_latitude else 'W'
    decimal = abs(decimal)
    degrees = int(decimal)
    minutes = int((decimal - degrees) * 60)
    seconds = (decimal - degrees - minutes / 60) * 3600
    return f'{degrees}°{minutes}\'{seconds:.2f}"{direction}'

def out_of_china(lat, lon):
    return lon < 72.004 or lon > 137.8347 or lat < 0.8293 or lat > 55.8271

if __name__ == "__main__":
    lat = 39.90960456049752
    lon = 116.3972282409668

    # WGS84 to GCJ-02
    gcj02 = wgs84_to_gcj02(lat, lon)
    print("WGS84 to GCJ-02: ", gcj02)

    # GCJ-02 to BD-09
    bd09 = gcj02_to_bd09(gcj02[0], gcj02[1])
    print("GCJ-02 to BD-09: ", bd09)

    # BD-09 to GCJ-02
    gcj02_from_bd09 = bd09_to_gcj02(bd09[0], bd09[1])
    print("BD-09 to GCJ-02: ", gcj02_from_bd09)

    # GCJ-02 to WGS84
    wgs84_from_gcj02 = gcj02_to_wgs84(gcj02_from_bd09[0], gcj02_from_bd09[1])
    print("GCJ-02 to WGS84: ", wgs84_from_gcj02)

    # WGS84 to BD-09
    bd09_from_wgs84 = wgs84_to_bd09(lat, lon)
    print("WGS84 to BD-09: ", bd09_from_wgs84)

    # BD-09 to WGS84
    wgs84_from_bd09 = bd09_to_wgs84(bd09_from_wgs84[0], bd09_from_wgs84[1])
    print("BD-09 to WGS84: ", wgs84_from_bd09)

    # CGCS2000 to WGS84
    wgs84_from_cgcs2000 = cgcs2000_to_wgs84(lat, lon)
    print("CGCS2000 to WGS84: ", wgs84_from_cgcs2000)

    # WGS84 to CGCS2000
    cgcs2000_from_wgs84 = wgs84_to_cgcs2000(lat, lon)
    print("WGS84 to CGCS2000: ", cgcs2000_from_wgs84)

    # GCJ-02 to CGCS2000
    cgcs2000_from_gcj02 = gcj02_to_cgcs2000(gcj02[0], gcj02[1])
    print("GCJ-02 to CGCS2000: ", cgcs2000_from_gcj02)

    # CGCS2000 to GCJ-02
    gcj02_from_cgcs2000 = cgcs2000_to_gcj02(lat, lon)
    print("CGCS2000 to GCJ-02: ", gcj02_from_cgcs2000)

    # WGS84 to UTM
    utm_coords = WGS84ToUTM(lat, lon)
    print(f"UTM: Easting: {utm_coords[0]}, Northing: {utm_coords[1]}, Zone Number: {utm_coords[2]}, Zone Letter: {utm_coords[3]}")

    # UTM to WGS84
    wgs84_coords = UTMToWGS84(utm_coords[0], utm_coords[1], utm_coords[2], utm_coords[3])
    print(f"WGS84: Latitude: {wgs84_coords[0]}, Longitude: {wgs84_coords[1]}")

    # DMS to Decimal
    dms_lat = "23°3'3.78\"N"
    dms_lon = "113°22'17.36\"E"
    decimal_coords = dms_to_decimal(dms_lat, dms_lon)
    print(f"Decimal: Latitude: {decimal_coords[0]}, Longitude: {decimal_coords[1]}")
    
    # Decimal to DMS
    dms_coords = decimal_to_dms(lat, lon)
    print(f"DMS: Latitude: {dms_coords[0]}, Longitude: {dms_coords[1]}")

以上代码实现了WGS84、GCJ-02、BD-09、CGCS2000和UTM坐标系之间的相互转换，以及Decimal(十进制经纬度)和DMS(度分秒经纬度)格式的相互转换。请注意，CGCS2000坐标系通常被认为与WGS84非常接近，因此在此示例中假设它们是等效的。根据具体的应用需求，可能需要更精确的转换方法。

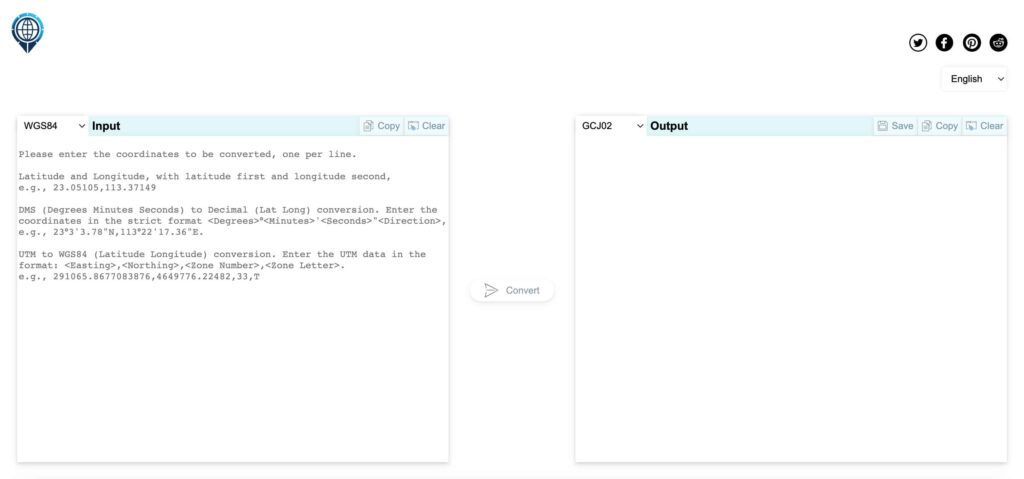
九、地理坐标系批量转化在线工具

看了下目前线上的转化工具，免费的只支持单个坐标的转化，批量转化还需要注册账号充值之后才可以用，而且一次性只能支持5000条。于是做了一个WGS84、GCJ-02、BD-09、CGCS2000和UTM之间两两互相转化的在线工具，也支持DMS（度分秒）和Decimal（十进制）两种经纬度格式的互转：https://latlongconverter.online/，支持单个和批量的经纬度坐标系转化，批量转化最大支持10万行数据，支持转化之后的数据一键复制或保存为Excel文档。

网站使用Vercel服务器运行，也用Cloudflare加速了，但因为部署在美国，国内网络访问首次加载可能比较慢，有开VPN的话加载速度很快，不影响使用。

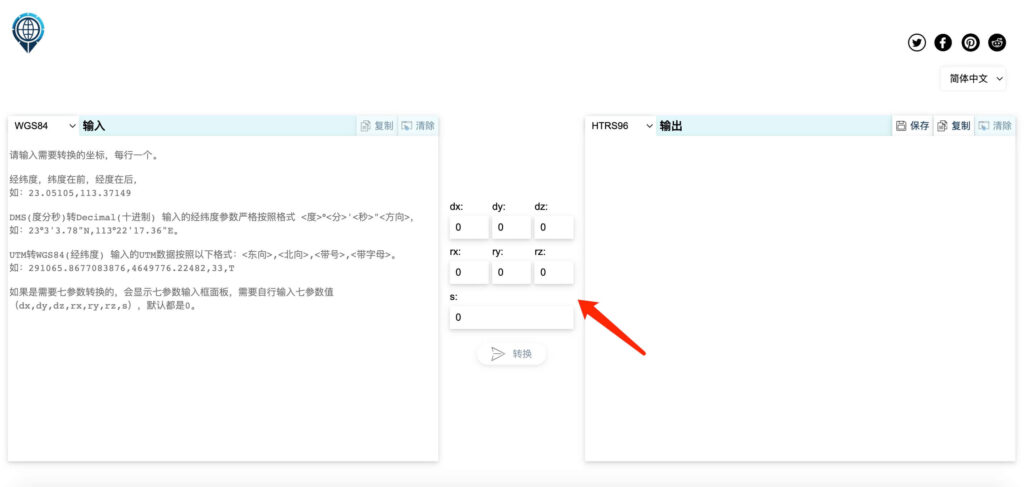
另：在2024.8.11新增了ETRS89、JGD2011、JGD2000、PRS92、ED50、HTRS96、GDM2000、Clarke 1880、BJ54、Indian 1975坐标和WGS84互转的功能，对于这些坐标的说明已在 https://latlongconverter.online/ 网站输入框下方列出，此处不再贴重复的内容说明。

新增的坐标大多需要做七参数转换，需要七参数输入的时候会在转换按钮上方显示七参数输入框面板，七参数转换需要的参数是保密的，网站只是提供一个转换功能支持，网站也不会保存用户任何的转换坐标数据和七参数数据。

BJ54和WGS84之间也需要七参数进行转换，WGS84可以等价CGCS2000坐标，如果需要BJ54转CGCS2000，可以直接使用BJ54和WGS84互转的功能。

9.1 七参数定义说明

七参数转换是一种常用的地理坐标系之间的转换方法，用于将一个参考椭球上的坐标转换到另一个参考椭球。这个转换模型包括三个平移参数、三个旋转参数和一个尺度参数，总共七个参数，因此称为“七参数”。

9.1.1 平移参数（Translation Parameters）

• dx：沿X轴方向的平移，单位为米（m）。

• dy：沿Y轴方向的平移，单位为米（m）。

• dz：沿Z轴方向的平移，单位为米（m）。

9.1.2 旋转参数（Rotation Parameters）

• rx：绕X轴的旋转角度，单位为弧度（rad）。有时也以秒为单位，需要将其转换为弧度使用。

• ry：绕Y轴的旋转角度，单位为弧度（rad）。

• rz：绕Z轴的旋转角度，单位为弧度（rad）。

9.1.3 尺度参数（Scale Parameter）

• s：尺度因子，通常以百万分之一（ppm, parts per million）为单位。如果尺度因子为1ppm，那么尺度因子的值为 s = 1 * 10^-6。

扩展阅读：

Android模拟定位实现详解

微信公众号

转载请注明出处：陈文管的博客 – WGS84、GCJ02、BD09、CGCS2000、UTM和BJ54地理坐标系详解及免费在线批量转换工具